Это копия тезисов моего доклада на международной конференции. Сохранил для истории 
MODERN TECHNIQUES AND MEASUREMENTS IN FLUID FLOWS
Proceedings of the 3rd International Conference on Fluid Dynamic Measurement and Its Applications
October 14-17, 1997
Beijing, China
EDITED BY
Shen Xiong
Sun Xijiu
1997
International Academic Publishers
(Moscow Power Engineering Institute — Technical University, Krasnokazarmennaya 17, Moscow, 111250, Russia, Fax: (095)-361-1620, E-mail: physics@mpei-rt.msk.su)
1. Abstract.
Research results of the cepstral method of the laser Doppler anemometer signals processing are presented. It is shown that this method can be used for a data reception on the size and concentration of scattering particles in researched areas of a flow. Also, the cepstral processing of the Doppler signals allows to reduce a particle velocity measurement error if by chance there are a large size of particles or multiparticles operation mode. The specified algorithms of an estimation of particle parameters are discussed.
2. Introduction.
At the moment laser Doppler anemometers (LDA) are widely used at a research of single-phase and two-phase flows of a liquid and gas (1,2). Usually LDA electronic processors work at a one-particle or multiparticle mode. At a one-particle operation mode only one particle can be in a measuring volume at any moment of time. At a multiparticle mode a laser light is diffracted by many particles simultaneously. In the first case Doppler signals are processed by a counter electronic processor, and in the second case — by a tracker.
A spectrum analyzer is a most universal electronic processor, which allows to carry out a processing of Doppler signals at a various concentration of scattering particles in a researched flow. The modern devices of this type represent specialized processors, which realize digital algorithms of the spectral analysis. The fast Fourier transform (FFT) of the input signal samples sequence is a basis of these algorithms. The Doppler frequency estimation is the frequency of the maximum envelope of the discret signal spectrum modulus, which is determined with a use of various interpolation methods. It turns out that in some instances the spectral method brings to a large frequency estimation error.
3. SIgnal models and processing methods.
We shall consider two-phase flows with such concentration of particles, at which the occurence of two scattering centres in the LDA measuring volume is most probable. In this case the Doppler signal is a sum of two Gaussian radiopulses to some superposition. The example of the temporary diagram of such signal is shown in fig. 1.
Let the superimposed pulses differ by their amplitude and moment of arrival. In that case the total Doppler signal is described by equation:
where S1(t) — the Gaussian radiopulse from one particle, A — the ratio of the pulse amplitudes, T -the time interval between the pulses. The spectral density of this signal will look like
where S1(jw) — the Gaussian radiopulse spectral density. The square of the total signal spectral density modulus will be equal
i.e. it is the product of the Gaussian radiopulse power spectrum by the periodic function. It is seen that the presence of the periodic function in equation (3) results to the oscillation of the curve |S2(jw)| and to the appearance of the additional local maxima of the Doppler spectrum modulus. The number of such maxima and their position on the frequency axis depend on the time interval T between the superimposed pulses. The diagram of the high-frequency component of the spectral density modulus of the signal represented in fig. 1 is shown in fig. 2. The analysis reveals that in a general case the presence of the LDA signal spectrum oscillation at the two-particle anemometer operation mode can result to the significant additional error of the Doppler frequency spectral estimation.
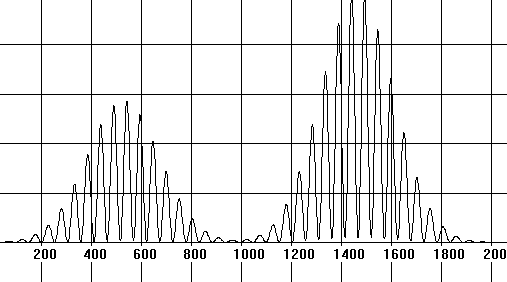
Fig.1. A typical temporary diagram of a two-particle signal
The researches (2,3) have shown that the similar situation arises at a processing of the signals, which are observed at a scattering by a single particle of a large size. In that case the oscillations of the signal spectrum modulus take place also. Their presence is not taken into account by existing algorithms of the Doppler frequency estimation and results to a growth of measurement errors. For the noncoherent model of a scattering2 the frequent interval between spectrum oscillations is connected directly to the size of a scattering particle.
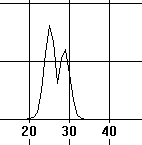
Fig.2. The two-particle signal spectrum
Thus, it is necessary to take into account the complex structure of the Doppler signal spectrum that allows to reduce the particle velocity estimation error and to receive the additional information on sizes or concentration of particles. The cepstral analysis is one of the methods of the single pulse spectrum restoration and estimation of the time interval between pulses. The given method was offered at the first time as a heuristic method for a determination of arrival moments of a compound signal reflection.
Usually, the cepstrum of function is determined as the power spectrum of the spectrum modulus square logarithm of this function4. Agrees equation (3) the logarithmic spectrum of the signal (1) looks like:
At A < 1 the third composed in the right part (4) can be written
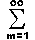[ (-1)m+1/m] (acoswT)m, (5)From equation (5) it follows that the logarithm of the power spectrum of the signal (1) contains the harmonic oscillations. Their amplitude and frequency are connected with the ratio A of the pulses amplitudes and the time delay T. The oscillation parameters are easily defined by means of the calculation of the spectrum of the given function, i.e. of the signal spectrum. Thus, according to equation (5), the time interval between the pulses corresponds to the moment of the first peak occurence in the power cepstrum. Besides the estimation of the power cepstrum of the elementary signal S1(t) can be obtained through an elimination of the cepstrum lateral peaks by a filtering. The logarithmic power spectrum of the elementary Doppler signal can be obtained through inverse FFT of the filtered cepstrum. It is clear that the additional local maxima will be away from such spectrum.
The capabilities of the given technique for an estimation of LDA signals parameters were investigated by a numerical modeling. The computer model took into account parameters of the LDA optical scheme, the number of particles in the LDA measuring volume, their sizes and trajectories of a movement. The cepstral processing was used in this model for the velocity estimation error decrease by a restoration of the elementary Doppler signal spectrum and for the determination of LDA operation mode, sizes of particles and distance between them. The processing algorithm provided a preliminary filtration of signal and account the cepstra of its high-frequency and low-frequency components. If the lateral peaks were present in the low-frequency component, it was agreed that the signal is the responce from several particles or from one, flying near by borders of the measuring volume. In case of absence of peaks the one-particle operation mode of LDA was registered. The cepstrum peaks in high-frequency component were observed at the signal processing both from several particles, and from one large particle. As this takes place the coordinate of the first lateral maximum of the Doppler signal cepstrum at a two-particle mode corresponded to a temporary interval between particles, and at an one-particle mode — a diameter of a particle.
4. Results and discussions.
The research of influence of the cepstral processing on the Doppler frequency estimation error of LDA signals by the spectral method have shown that a filtration of cepstrum gives appreciable positive results at the sizes of a large particle or distances between small particles more 1.5w0 (w0 — the radius of the probing beam) and at any nonzero phase shift between pulses. The signal-to-noise ratio can be rather small (up to 0 dB). At small levels of noise (signal-to-noise ratio 20 dB) the accuracy of measurements can be increased 50-100 times. The results of the cepstral processing are illustrated in fig. 3.
The diagrams of the results of the programm determination of the LDA operation mode at the different ratio of the Doppler signal amplitude in the centre of pulse to the root-mean-square value of additive noise on 20 independent statistical samples are shown in fig. 4. The relative number (in %) of determination results of an either mode (one small particle, one large particle, two small particles) at really given a one-particle operation mode and a small size of a particle is shown on the axis of ordinates. The analysis of the diagram shows that the cepstral processing can be used for the determination of operation mode at the signal-to-noise ratio on a voltage more than 30. At stronger noise it is not possible to determine a mode unequivocally.
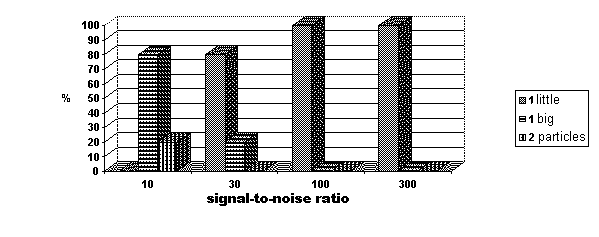
Fig.3. Determination of the LDA operation mode at presence of noise.
The dependence of the ratio of the distance S* between particles, measured with the application of cepstral processing, to the radius of laser beam w0 at two-particle LDA operation mode from the ratio of the given distance S to w0 is shown in fig. 4. The program determined a mode as one-particle if the interval between particles was less than 1.5w0. At S>2w0 the error of distance estimation has made less than 0.1%.
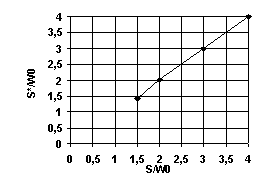
Fig.4. Estimation of the distance between particles by the cepstral method.
The dependence of the measured value of the particle radius on its real size, obtained by numerical modeling, is represented in fig.5. The ratio of the particle radius r, given at modeling, to the laser beam radius w0 is marked on an axis of abscisses. The ratio of an estimation of the particle radius to w0 is marked on the axis of ordinates. At account the beam radius was equal w0 = 50 micrometers, and the difference of frequencies of two probing beams was equal 30 MHz. The similar kind of dependence was observed at w0 = 100 micrometers and 200 micrometers. At r/w0<0.5…0.7 the algorithm did not discern a large particle or gave a wrong estimation of its radius.
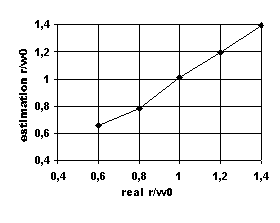
Fig.5. Estimation of the particle radius by cepstral method.
Thus, it is shown that the application of the LDA signals cepstral processing allows to increase essentially the accuracy of flow velocity measurements at the presence of significant disorder of the scattering particle parameters. Besides use of these algorithms allows to estimate the sizes and concentration of particles that represents a large interest at research of two-phase flows.
References.
[1] Rinkevichius B.S. Laser Diagnostics in Fluid Mechanics. 1990, MPEI Press, Moscow /in Russian/.
[2] Karasyk A.Ya., Rinkevichius B.S., and Zubov V.A. Laser Interferometry Principles /Ed. B.S.Rinkevichius. 1995, Mir Publishers and CRC Press, Moscow and London.
[3] Grechikhin V.A., Rinkevichius B.S., Stepanov A.V., Tolkachev A.V., Kononenko V.L. «Complex structure of Doppler spectrum of a single large particle», In: Optical methods and Data Processing in Heat and Fluid Flow. London, Mechanical Engineering Publications Limited (1996), 393.
[4] Tikhomirova N.K., Tikhomirov A.G. On the influence of scattering particle size on signal frequency shift in laser Doppler spectrometer / Quantum electronics, Vol.15, 1 (1998), 218-222.
[5] D.G.Childers, D.P.Skinner, R.C.Kemerait. The Cepstrum: A Guide to Processing. Proc. IEEE, Vol. 65, 10 (1977), 1428-1443.
